比治山日記

比治山スカイウォーカーです

プロクラステス分析

統計

点群のレジストレーションや姿勢推定の論文で出てくるプロクラステス分析を知らなかったので調べて実装しました．

プロクラステス分析とは

プロクラステス分析（procrustes analysis，プロクラステス解析とも）は点同士の対応がとれた2つの点群に対して，並進・回転・一様なスケーリングの変換のもとで，点群間の二乗誤差が最小になるように重ねあわせする処理です．この記事では特に，回転行列が直交行列であるようなケースの直交プロクラステス分析(Orthogonal Procrustes analysis)について扱います．

方法

1. 2つの点群の重心を原点に位置合わせする

点群\bf X, Yの重心が原点になるよう，\bf X, Yからそれぞれの平均を引きます． \begin{equation} {\bf X}_{o} = {\bf X} - \overline{\bf X} \qquad {\bf Y}_{o} = {\bf Y} - \overline{\bf Y} \end{equation} 2. 2つの点群のスケールを正規化する

\begin{equation} {\bf X}_{norm} = \dfrac{{\bf X_o}}{||{\bf X}_o||_F} \qquad {\bf Y}_{norm} = \dfrac{{\bf Y_o}}{||{\bf Y}_o||_F} \end{equation} 3. 回転に二乗誤差が最小になるように回転する

重心を原点に位置合わせし，スケールを正規化した2つの点群を改めて\bf A, Bとします．すると， {\bf A}を回転して誤差が最小になるように {\bf B}に重ねあわせる時の回転行列 {\bf R}は以下の式で求めることができます． \begin{equation}
{\bf R} = argmin_{\bf \Omega}{|| {\bf \Omega A} - {\bf B} ||}_F \quad s.t. \quad {\bf \Omega}^{T} {\bf \Omega} = I \end{equation}

この式は
\begin{equation} ||{\bf \Omega A} - {\bf B}||^2_F = ||{\bf A}||^2_F + ||{\bf B}||^2_F - 2 \langle {\bf \Omega A}, {\bf B}\rangle \end{equation} と変形でき、これを最小化するには右辺第三項を最大化します．次にこの項を以下のように変形します．

\begin{align*} \langle{\bf \Omega A}, {\bf B}\rangle &= tr({\bf A^T \Omega^T B}) = tr({\bf B^T \Omega A}) = tr({\bf \Omega A B^T}) \newline &= tr({\bf \Omega USV^T})= tr({\bf SV^T\Omega U})
\end{align*} となります． （ただし {\bf A B^T}={\bf USV^T}と特異値分解した．）

{\bf X} = {\bf V^T\Omega U}と置くと，この右辺は直交行列の積であることから \bf Xは直交行列になり，式は以下のように変形できます．
\begin{equation} tr({\bf SV^T\Omega U}) = tr({\bf SX}) = \sum_i s_{ii}x_{ii}
\end{equation} s_{ii}は特異値であるため非負になるので，この式を最大化する直交行列は明らかに {\bf X} = {\bf I}の時です． よって {\bf X} = {\bf I} = {\bf V^T\Omega U}であるため {\bf \Omega} = {\bf VU^T}の時，当初の式が最小化されるのでこれが求めたい回転行列 \bf Rになります．

実装

実装は↓にあるけど，ためしに自分でも実装してみました． stackoverflow.com

自分の実装

import numpy as np

def procrustes(x, y):
    """
    Orthogonal procrustes analysis

    Inputs:
    ------------
    X, Y    
        matrices of target and input coordinates. 

    Outputs
    ------------
    Z
        the matrix of transformed X-values
    """
    mux = np.mean(x, axis=0)
    muy = np.mean(y, axis=0)
    X = x - mux
    Y = y - muy
    X_norm = np.linalg.norm(X) # frobenius norm
    Y_norm = np.linalg.norm(Y) # frobenius norm
    normalized_X = X / X_norm
    normalized_Y = Y / Y_norm
    
    u, w, vt = np.linalg.svd(np.dot(normalized_X, normalized_Y.T))
    
    R = np.dot(vt.T, u.T)
    scale = w.sum() * X_norm / Y_norm
    Z = Y_norm * w.sum() * np.dot(R, normalized_X) + muy 
    
    return Z

二次元の点群に対して回転・並進・スケーリングした上で各点にガウスノイズを加えてできた点群と，もとの点群でプロクラステス分析した結果が次の図です． f:id:exv:20171024221928p:plain

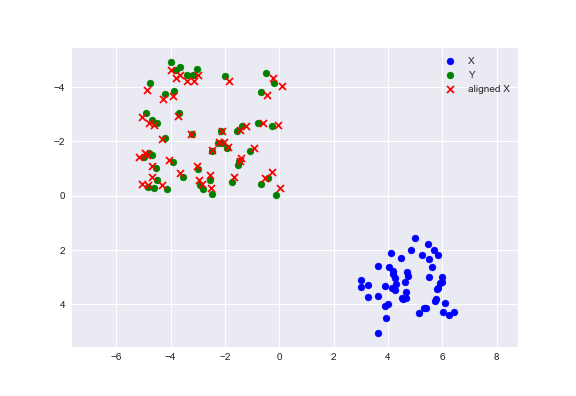
補足

プロクラステス分析は2点群間の対応が取れているのに対して，ICP(Iterative Closest Point)は一般に揃えたい点群間の対応が取れていない場合や点数が異なるケースを扱っている（大規模な点群の一部分に位置合わせしたい，など）という違いがあるようです．

参考資料

[1] Ross, A. "Procrustes analysis." Course report, Department of Computer Science and Engineering, University of South Carolina (2004).
[2] Akça, M. Mehmet, D. "Generalized procrustes analysis and its applications in photogrammetry." (2003).